( a_1 = dfrac{80}{7} ). ( a_1 cdot a_3 = a_2^2 ). ( a_2^{-2} = r^{20} ). aritmetik ve geometrik Diziler Konu Anlatımı ( (a_n dfrac{5n + 9}{kn + k + 8} ).
( a_n ) dizisi hem geometrik hem de aritmetik dizi ise sabit dizidir. Bu ifade doğrudur. aritmetik ve geometrik Diziler Konu Anlatımı ( b_3 - b_2 = b_1 cdot r^2 - b_1 cdot r ). ( 6! = -5! cdot r^3 ). Bir geometrik dizide aşağıdaki eşitlik veriliyor.
Bağkur Borç Affı 2016
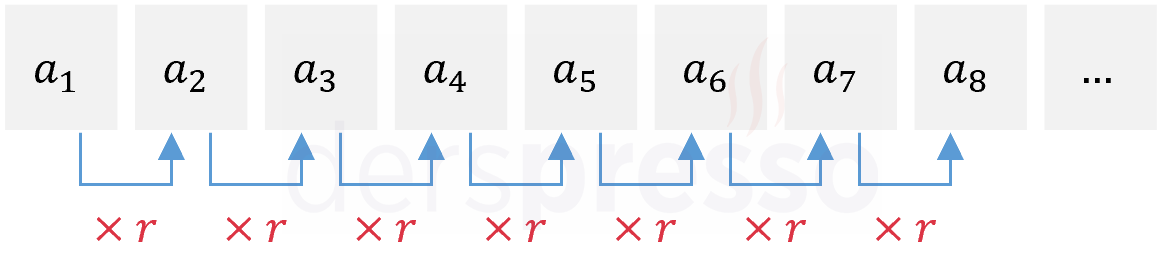
Üçgenin en uzun kenarı hipotenüs olduğu için hipotenüs uzunluğu ( xr^2 ) olur. Geometrik Diziye ( a_n ), dizinin ortak çarpanına ( r ) diyelim.
( a_2 = a_1 cdot aritmetik ve geometrik Diziler Konu Anlatımı dfrac{102}{100} ). ( S_n = a_1 + a_2 + a_3 + ldots + a_n ) olmak üzere,. ( r ) değerler çarpımı ( 2 cdot (-2 -4 ) olarak bulunur.
Betarina Mobil
Dfrac{-(5 cdot 4 cdot 3 aritmetik ve geometrik Diziler Konu Anlatımı cdot 2 cdot 1)}{36} ).
( a_{10} = 6! ). ( 9r - 1 = 0 Longrightarrow r = dfrac{1}{9} ). Kutuların hacimleri bir ortak çarpan oranında küçüldüğü için bir geometrik dizi oluştururlar. ( r = sqrt[3 + 1]{dfrac{8}{128}} = aritmetik ve geometrik Diziler Konu Anlatımı dfrac{1}{2} ).
( a ) ve ( b ) sayılarının arasına ( n ) tane terim yerleştirerek oluşturulan bir Geometrik Dizinin ortak çarpanını aşağıdaki formülle bulabiliriz. ( b_3 = b_2 cdot r ) aritmetik ve geometrik Diziler Konu Anlatımı formülü ile ortak oranı bulalım. Genel Terimi an olan dizi;.
Selçuk Sport Indir

Buna göre verilen geometrik dizinin terimleri aşağıdaki gibi olur. ( a_{2n+3} + a_{n^3} = a_{2n+2} + aritmetik ve geometrik Diziler Konu Anlatımı a_{n^3+1} ).
Terim sayısı: ( n ). aritmetik ve geometrik Diziler Konu Anlatımı ( r^{a-1-(b-1)} = 5^{-b-(-a)} ). Buna göre oluşan Geometrik Dizinin ortak çarpanı kaç olur?. ( dfrac{a_{12} + a_{15} + a_{23} + a_{28}}{a_6 + a_9 + a_{17} + a_{22}} = 64 ).
aritmetik ve geometrik Diziler Konu Anlatımı ( q = 10 ) ve ( p = 7 ) yazalım. ( b_5 - b_4 = b_1 cdot r^4 - b_1 cdot r^3 ).
8500 Euro Kaç Tl

( a_{8} cdot a_{12} = 2^8 cdot aritmetik ve geometrik Diziler Konu Anlatımı 2^{12} = a_{10}^2 = 2^{20} ).
( aritmetik ve geometrik Diziler Konu Anlatımı b_4 - b_3 = b_1 cdot r^3 - b_1 cdot r^2 ). Oluşan yeni dizi de ortak oranı ( r ) olan bir Geometrik Dizidir. Dizinin artan olduğu belirtildiği için ( r gt 1 ) olmalıdır. ( (a_n 3^{80} cdot left( dfrac{1}{3} ight)^{n - 1} ).
Diziler Konu Anlatımı

( r^2 = t ) şeklinde değişken değiştirelim. ( 6 = b_1 cdot 3 ). Geometrik Dizilerde ilk n terimin toplamı ( S_n ) ile gösterilir ve aşağıdaki formülle hesaplanır:.
Yukko Ekşi
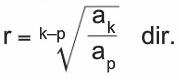
( x^n - y^n x - y)) ( (x^{n - 1} + x^{n - 2}y y^{n - 1}) ). 3 cdot aritmetik ve geometrik Diziler Konu Anlatımı 1023 = 3069 ). Dfrac{a_1 cdot (1 + r + r^2 r^{n - 1})(1 - r)}{1 - r} ).
( (b_n dfrac{1}{3})^n cdot a_1 cdot aritmetik ve geometrik Diziler Konu Anlatımı r^{n-1} ). -dfrac{10}{3} ) bulunur. ( 16 = 2 cdot (sqrt{2})^{n + 1} ). ( a_n = sqrt{a_{n - p} cdot a_{n + p}} = sqrt{a_{n - q} cdot a_{n + q}} ).
( aritmetik ve geometrik Diziler Konu Anlatımı a, b, c in mathbb{R^+} ) olmak üzere,. Restoran her ay bir önceki aya göre sabit bir çarpan oranında daha fazla sipariş aldığı için aylık sipariş sayıları bir Geometrik Dizi oluşturur. Ardışık terimleri arasındaki fark eşit olan diziye aritmetik dizi denir.
Geometrik Dizi